A right-angled cone (with base radius $5$ cm and height $12$ cm), as shown in the figure below, is rolled on the ground keeping the point $P$ fixed until the point $Q$ (at the base of the cone, as shown) touches the ground again.
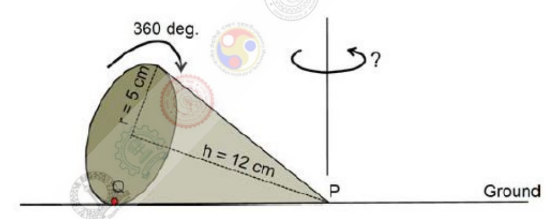
By what angle (in radians) about $P$ does the cone travel?
- $\dfrac{5\pi}{12} \\$
- $\dfrac{5\pi}{24} \\$
- $\dfrac{24\pi}{5} \\$
- $\dfrac{10\pi}{13}$