The growth of bacteria (lactobacillus) in milk leads to curd formation. A minimum bacterial population density of $0.8$ (in suitable units) is needed to form curd. In the graph below, the population density of lactobacillus in $1$ litre of milk is plotted as a function of time, at two different temperatures, $25^{\circ}$C and $37^{\circ}$C.
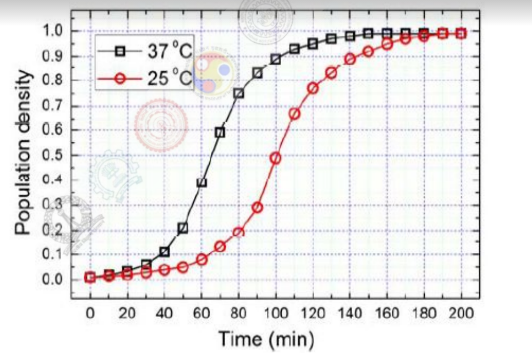
Consider the following statements based on the data shown above:
- The growth in bacterial population stops earlier at $37^{\circ}$C as compared to $25^{\circ}$C
- The time taken for curd formation at $25^{\circ}$C is twice the time taken at $37^{\circ}$C
Which one of the following options is correct?
- Only $i$.
- Only $ii$.
- Both $i$ and $ii$.
- Neither $i$ nor $ii$