GATE Mechanical 2022 Set 1 | GA Question: 3

Question

A person travelled $80$ $\text{km}$ in $6$ hours. If the person travelled the first part with a uniform speed of $10$ $\text{kmph}$ and the remaining part with a uniform speed of $18$ $\text{kmph}$.

What percentage of the total distance is travelled at a uniform speed of $10$ $\text{kmph}$?

• A. $28.25$
• B. $37.25$
• C. $43.75$
• D. $50.00$

Answer 1

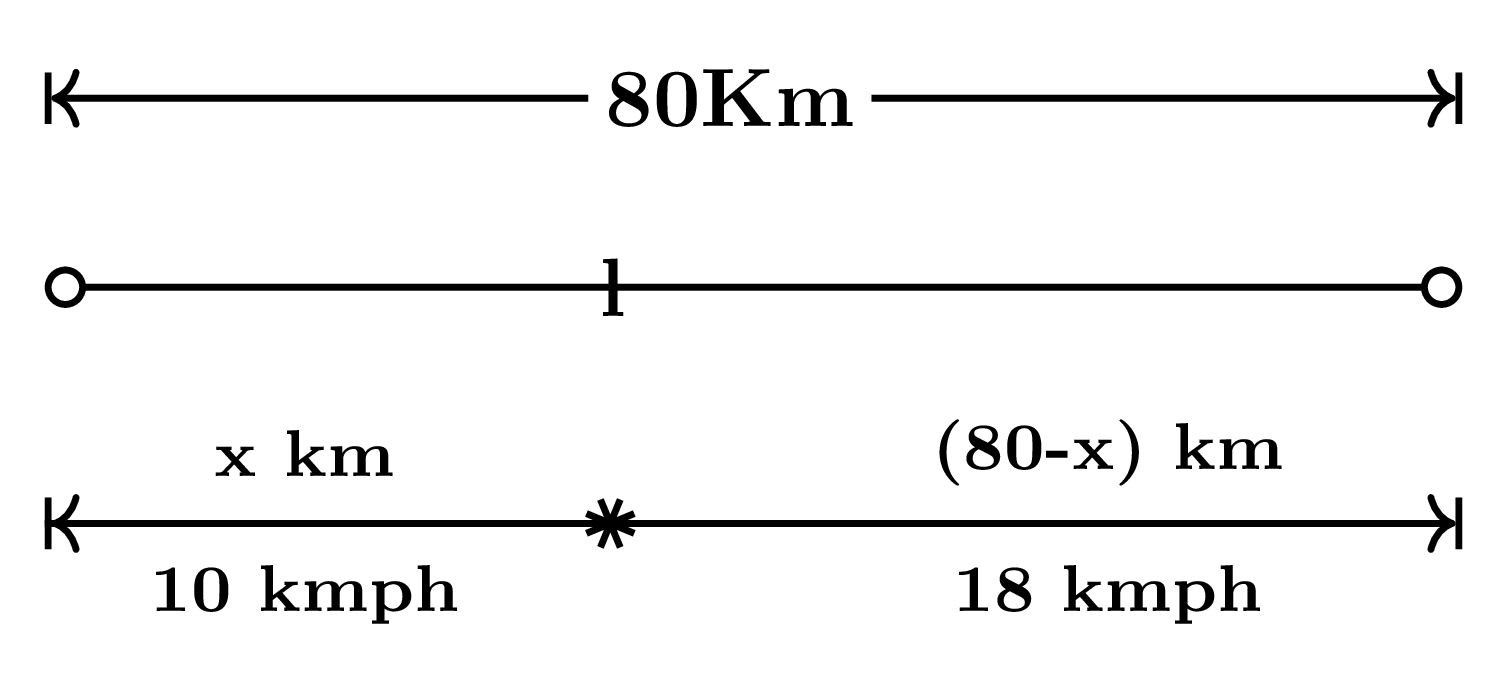
Let the distance traveled (first part) by the person at a uniform speed of $10$ kmph be $x$ km.
 

We know that, ${\color{Green}{\text{Speed} = \dfrac{\text{Distance}}{\text{Time}}}}$

$\implies {\color{Lime}{\boxed{\text{Time} = \dfrac{\text{Distance}}{\text{Speed}}}}}$

Now, $\dfrac{x}{10} + \dfrac{(80-x)}{18} = 6$

$\Rightarrow \dfrac{18x + 800 – 10x}{180} = 6$

$\Rightarrow 8x = 1080- 800$

$\Rightarrow 8x = 280$

$\Rightarrow {\color{Blue}{\boxed{x = 35\;\text{km}}}}$

$\therefore$ The percentage of the total distance is traveled at a uniform speed of $10$ kmph $ = \dfrac{35}{80} \times 100\% = 43.75\%.$

Correct Answer $:\text{C}$