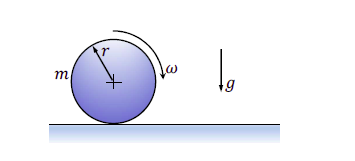
A cylindrical disc of $\text{mass m = 1 kg}$ and $\text{radius r = 0.15 m}$ was spinning at $\omega =5\; rad/s$ when it was placed on a flat horizontal surface and released (refer to the figure). Gravity $g$ acts vertically downwards as shown in the figure. The coefficient of friction between the disc and the surface is finite and positive. Disregarding any other dissipation except that due to friction between the disc and the surface, the horizontal velocity of the center of the disc, when it starts rolling without slipping, will be __________________$m/s$ (round off to $2$ decimal places).