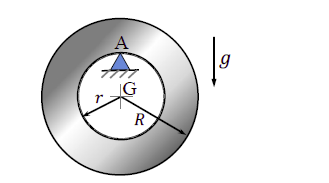
A rigid uniform annular disc is pivoted on a knife edge $A$ in a uniform gravitational field as shown, such that it can execute small amplitude simple harmonic motion in the plane of the figure without slip at the pivot point. The inner radius $r$ and outer radius $R$ are such that $r^{2} = \frac{R^{2}}{2}$, and the acceleration due to gravity is $g$. If the time period of small amplitude simple harmonic motion is given by $T = \beta \pi \sqrt{\frac{R}{g}}$, where $\pi$ is the ratio of circumference to diameter of a circle, then $\beta = $ ____________________ (round off to $2$ decimal places).