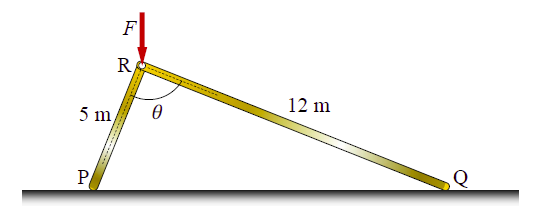
Two rigid massless rods $PR$ and $RQ$ are joined at frictionless pin-joint $R$ and are resting on ground at $P$ and $Q$, respectively, as shown in the figure. A vertical force $F$ acts on the pin $R$ as shown. When the included angle $\theta < 90^{\circ}$, the rods remain in static equilibrium due to Coulomb friction between the rods and ground at locations $P$ and $Q$. At $\theta = 90^{\circ}$, impending slip occurs simultaneously at points $P$ and $Q$. Then the ratio of the coefficient of friction at $Q$ to that at $P\left(\mu_{Q}/\mu_{P}\right)$ is ___________________ (round off to two decimal places).