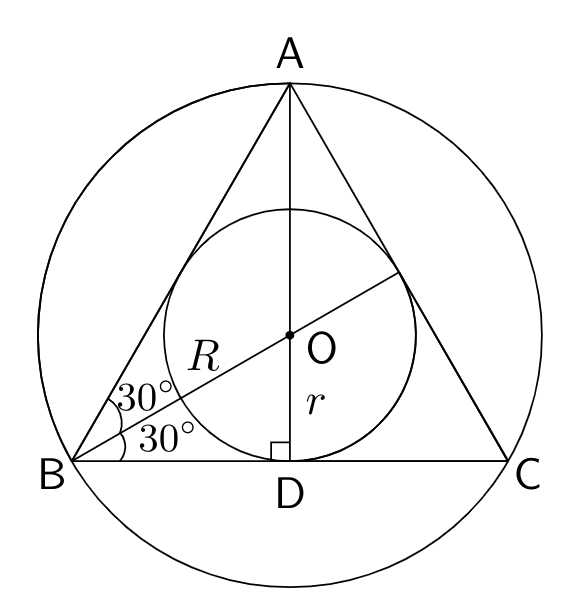
Given that, the $\triangle ABC$ is an equilateral triangle.
Let the radius of the inscribed circle be $r\;\text{cm},$ and radius of the circumscribed circle be $R\;\text{cm}.$
In $\triangle OBD,\angle OBD = 30^{\circ},\angle ODB = 90^{\circ}$
$\implies \sin 30^{\circ} = \dfrac{r}{R} $
$\implies\dfrac{1}{2}= \dfrac{r}{R}$
$\implies R = 2r$
Let the area of the inscribed circle be $A_{I}\;\text{cm}^{2}$ and the area of the circumscribed circle be $A_{C}\;\text{cm}^{2}.$
$\implies \dfrac{A_{I}}{A_{C}} = \dfrac{\pi r^{2}}{\pi R^{2}} = \dfrac{r^{2}}{(2r)^{2}} = \dfrac{1}{4}.$
So, the correct answer is $(C).$