Register

GATE2017 ME-2: 40

• recategorized by
715 views
0 0 votes

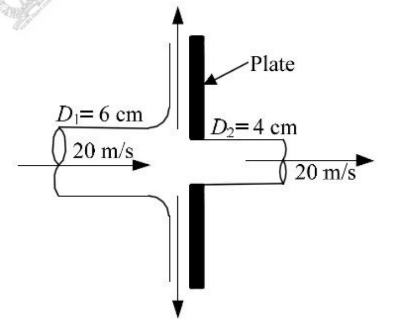
A $60$ mm-diameter water jet strikes a plate containing a hole of $40$ mm diameter as shown in the figure. Part of the jet passes through the hole horizontally and the remaining is deflected vertically. The density of water is $1000 kg/m^{3}$. If velocities are as indicated in the figure, the magnitude of horizontal force (in N) required to hold the plate is _________.

Please log in or register to answer this question.

Related questions

0 0 votes
0 0 answers
485
485 views
Arjun asked Feb 26, 2017
485 views
GATE2017 ME-2: 39
The arrangement shown in the figure measures the velocity $V$ of a gas of density $1 kg/m^{3}$ flowing through a pipe. The acceleration due to gravity is $9.81 m/s^{2}$. ...
0 0 votes
0 0 answers
305
305 views
Arjun asked Feb 26, 2017
305 views
GATE2017 ME-2: 41
For the laminar flow of water over a sphere, the drag coefficient $C_{F}$ is defined as $C_{F}=F/(\rho U^{2} D^{2})$, where $F$ is the drag force, $\rho$ is the fluid den...
0 0 votes
0 0 answers
419
419 views
Arjun asked Feb 26, 2017
419 views
GATE2017 ME-1: 8
Water (density $= 1000 kg/m^{3}$) at ambient temperature flows through a horizontal pipe of uniform cross section at the rate of $1 kg/s$. If the pressure drop across the...
0 0 votes
0 0 answers
508
508 views
Arjun asked Feb 9, 2019
508 views
GATE2019 ME-2: 23
Water enters a circular pipe of length $L=5.0$ m and diameter $D=0.20$m with Reynolds number $Re_D=500$. The velocity profile at the inlet of the pipe is uniform while it...
Voting & Accepting an answer helps improve the community

Related questions

0 0 votes
0 0 answers
485
485 views
Arjun asked Feb 26, 2017
485 views
GATE2017 ME-2: 39
The arrangement shown in the figure measures the velocity $V$ of a gas of density $1 kg/m^{3}$ flowing through a pipe. The acceleration due to gravity is $9.81 m/s^{2}$. ...
0 0 votes
0 0 answers
305
305 views
Arjun asked Feb 26, 2017
305 views
GATE2017 ME-2: 41
For the laminar flow of water over a sphere, the drag coefficient $C_{F}$ is defined as $C_{F}=F/(\rho U^{2} D^{2})$, where $F$ is the drag force, $\rho$ is the fluid den...
0 0 votes
0 0 answers
419
419 views
Arjun asked Feb 26, 2017
419 views
GATE2017 ME-1: 8
Water (density $= 1000 kg/m^{3}$) at ambient temperature flows through a horizontal pipe of uniform cross section at the rate of $1 kg/s$. If the pressure drop across the...
0 0 votes
0 0 answers
508
508 views
Arjun asked Feb 9, 2019
508 views
GATE2019 ME-2: 23
Water enters a circular pipe of length $L=5.0$ m and diameter $D=0.20$m with Reynolds number $Re_D=500$. The velocity profile at the inlet of the pipe is uniform while it...
← Previous · GATE2017 ME-2: 39Next → · GATE2017 ME-2: 41
← Previous in category · GATE2017 ME-2: 39Next in category → · GATE2017 ME-2: 41
Position:
Show:
Answer:

Add Synced Question

×