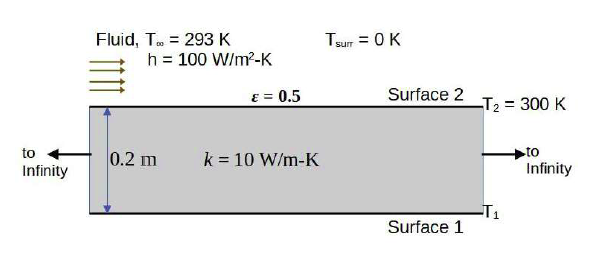
Consider a solid slab (thermal conductivity, $k = 10\; W \cdot m^{-1}\cdot K^{-1})$ with thickness $0.2\; m$ and of infinite extent in the other two directions as shown in the figure. Surface $2$, at $300 K$, is exposed to a fluid flow at a free stream temperature ${\left(T_{\infty}\right)}$ of $293 K$, with a convective heat transfer coefficient $(h)$ of $100 W \cdot m^{-2}\cdot K^{-1}$. Surface $2$ is opaque, diffuse and gray with an emissivity $(\varepsilon)$ of $0.5$ and exchanges heat by radiation with very large surroundings at $0\; K$. Radiative heat transfer inside the solid slab is neglected. The Stefan-Boltzmann constant is $5.67 \times 10^{-8} W \cdot m^{-2} \cdot k^{-4}$. The temperature $T_{1}$ of Surface $1$ of the slab, under steady-state conditions, is ______________ $K$ (round off to the nearest integer).