A thin-walled cylinder of radius $r$ and thickness $t$ is open at both ends, and fits snugly between two rigid walls under ambient conditions, as shown in the figure.
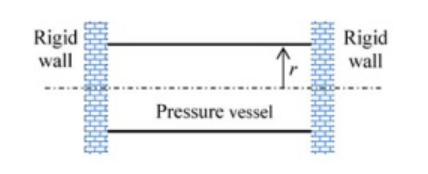
The material of the cylinder has Young’s modulus $E$, Poisson’s ratio $v$, and coefficient of thermal expansion $\alpha$. What is the minimum rise in temperature $\Delta T$ of the cylinder (assume uniform cylinder temperature with no buckling of the cylinder) required to prevent gas leakage if the cylinder has to store the gas at an internal pressure of $p$ above the atmosphere?
- $\Delta T = \dfrac{3vpr}{2 \alpha t E} \\$
- $\Delta T = \big( v – \dfrac{1}{4} \big) \dfrac{pr}{ \alpha t E} \\$
- $\Delta T = \dfrac{vpr}{\alpha t E} \\$
- $\Delta T = \big( v + \dfrac{1}{2} \big) \dfrac{pr}{ \alpha t E} $