Register

GATE2020-ME-2: 29

• edited by
0 votes
0 votes

The sun (S) and the Planet (P) of an epicyclic gear train shown in the figure have identical number of teeth.

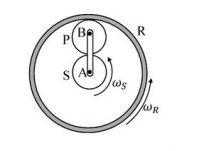
If the sun (S) and the outer ring (R) gears are rotated in the same direction with angular speed $\omega_S$ and $\omega_R$, respectively, then the angular speed of the arm $AB$ is

  1. $\dfrac{3}{4} \omega _R + \dfrac{1}{4} \omega _S \\$
  2. $\dfrac{1}{4} \omega _R + \dfrac{3}{4} \omega _S \\$
  3. $\dfrac{1}{2} \omega _R - \dfrac{1}{2} \omega _S \\$
  4. $\dfrac{3}{4} \omega _R - \dfrac{1}{4} \omega _S $
• edited by

Please log in or register to answer this question.

← PreviousNext →
← Previous in categoryNext in category →
Answer:

Related questions

0 answers
0 votes
go_editor asked Sep 18, 2020
GATE2020-ME-2: 11
Which one of the following statements about a phase diagram is INCORRECT? It indicates the temperature at which different phases start to melt Relative amount of different phases can be found under given equillibrium conditions It gives information on transformation rates Solid solubility limits are depicted by it
Which one of the following statements about a phase diagram is INCORRECT?It indicates the temperature at which different phases start to meltRelative amount of different ...
0 answers
0 votes
go_editor asked Sep 18, 2020
GATE2020-ME-2: 13
In Materials Requirement Planning, if the inventory holding cost is very high and the set up cost is zero, which one of the following lot sizing approaches should be used? Economic Order Quantity Lot-for-Lot Base Stock Level Fixed Period Quantity, for $2$ periods
In Materials Requirement Planning, if the inventory holding cost is very high and the set up cost is zero, which one of the following lot sizing approaches should be used...
0 answers
0 votes
go_editor asked Sep 18, 2020
GATE2020-ME-2: 15
In the space above the mercury column in a barometer tube, the gauge pressure of the vapour is positive, but more than one atmosphere negative zero positive, but less than one atmosphere
In the space above the mercury column in a barometer tube, the gauge pressure of the vapour ispositive, but more than one atmospherenegativezeropositive, but less than on...
Voting & Accepting an answer helps improve the community
Link Copied!