GATE2017 ME-2: 38

Question

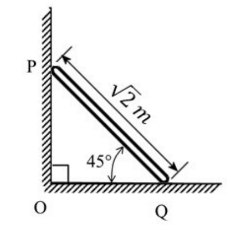
The rod $PQ$ of length $L=\sqrt{2}$ m, and uniformly distributed mass of $M=10$ kg, is released from rest at the position shown in the figure. The ends slide along the frictionless faces $OP$ and $OQ$. Assume acceleration due to gravity, $g=10 m/s^{2}$. The mass moment of inertia of the rod about its centre of mass and an axis perpendicular to the plane of the figure is $(ML^{2}/12)$. At this instant, the magnitude of angular acceleration (in radian/$s^{2}$) of the rod is __________.