Register

GATE2016-2-41

• recategorized by
0 votes
0 votes

Consider a frictionless, massless and leak-proof plug blocking a rectangular hole of dimensions $2R \times L$ at the bottom of an open tank as shown in the figure. The head of the plug has the shape of a semi-cylinder of radius $R$. The tank is filled with a liquid of density $\rho$ up to the tip of the plug. The gravitational acceleration is $g$. Neglect the effect of the atmospheric pressure.

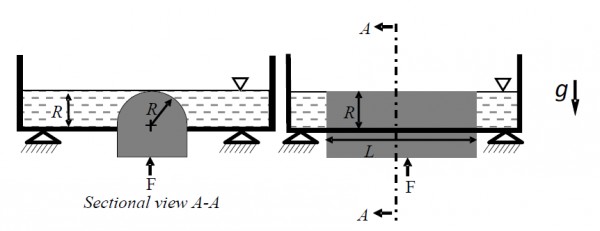
The force $F$ required to hold the plug in its position is

  1. $2\rho R^2gL(1-\dfrac{\pi }{4}) \\$
  2. $2\rho R^2gL(1+\dfrac{\pi }{4}) \\$
  3. $\pi R^2\rho gL \\$
  4. $\dfrac{\pi }{2}\rho R^2gL$
• recategorized by
User Avatar

Please log in or register to answer this question.

← PreviousNext →
← Previous in categoryNext in category →
Answer:

Related questions

0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2016-2-21
In the phase diagram shown in the figure, four samples of the same composition are heated to temperatures marked by $a, b, c$ and $d$. At which temperature will a sample get solutionized the fastest? $a$ $b$ $c$ $d$
In the phase diagram shown in the figure, four samples of the same composition are heated to temperatures marked by $a, b, c$ and $d$.At which temperature will a sample g...
0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2016-2-53
For the situation shown in the figure below the expression for $H$ in terms of $r$, $R$ and $D$ is $H=D+\sqrt{r^2+R^2}$ $H=(R+r)+(D+r)$ $H=(R+r)+\sqrt{D^2-R^2}$ $H=(R+r)+\sqrt{2D(R+r)-D^2}$
For the situation shown in the figure below the expression for $H$ in terms of $r$, $R$ and $D$ is $H=D+\sqrt{r^2+R^2}$$H=(R+r)+(D+r)$$H=(R+r)+\sqrt{D^2-R^2}$$H=(R+r)+\sq...
0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2016-2-52
The surface irregularities of electrodes used in an electrochemical machining (ECM) process are $3 \: μm$ and $6 \: μm$ as shown in the figure. If the work-piece is of pure iron and $12V \: DC$ ... $F_e^{+2}$ and the Faraday constant to be $96500$ Coulomb.
The surface irregularities of electrodes used in an electrochemical machining (ECM) process are $3 \: μm$ and $6 \: μm$ as shown in the figure. If the work-piece is of ...
Voting & Accepting an answer helps improve the community
Link Copied!