Register

GATE2016-1-8

• recategorized by
0 votes
0 votes

The cross sections of two hollow bars made of the same material are concentric circles as shown in the figure. It is given that $r_3>r_1$ and $r_4 > r_2$, and that the areas of the cross-sections are the same. $J_1$ and $J_2$ are the torsional rigidities of the bars on the left and right, respectively. The ratio $\displaystyle{\frac{J_2}{J_1}}$ is

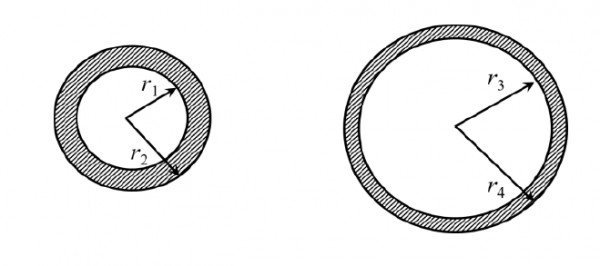
  1. $>1$
  2. $<0.5$
  3. $=1$
  4. between $0.5$ and $1$
• recategorized by
User Avatar

Please log in or register to answer this question.

← PreviousNext →
← Previous in categoryNext in category →
Answer:

Related questions

0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2016-1-52
A $300$ $mm$ thick slab is being cold rolled using roll of $600$ $mm$ diameter. If the coefficient of friction is $0.08$, the maximum possible reduction (in $mm$) is __________
A $300$ $mm$ thick slab is being cold rolled using roll of $600$ $mm$ diameter. If the coefficient of friction is $0.08$, the maximum possible reduction (in $mm$) is ____...
0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2016-1-33
The figure shows cross-section of a beam subjected to bending. The area moment of inertia (in $mm^4$) of this cross-section about its base is ________
The figure shows cross-section of a beam subjected to bending. The area moment of inertia (in $mm^4$) of this cross-section about its base is ________
Voting & Accepting an answer helps improve the community
Link Copied!