GATE2015-3-4

Question

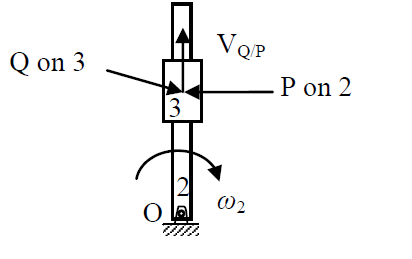
In the figure, link $2$ rotates with constant angular velocity $\omega_2$. A slider link $3$ moves outwards with a constant relative velocity $V_{Q/P}$, where $Q$ is a point on slider $3$ and $P$ is a point on link $2$. The magnitude and direction of Coriolis component of acceleration is given by

• A. $2 \omega_2$ $V_{Q/P}$; direction of $V_{Q/P}$ rotated by $90^\circ$ in the direction of $\omega_2$
• B. $\omega_2$ $V_{Q/P}$; direction of $V_{Q/P}$ rotated by $90^\circ$ in the direction of $\omega_2$
• C. $2 \omega_2$ $V_{Q/P}$; direction of $V_{Q/P}$ rotated by $90^\circ$ opposite to the direction of $\omega_2$
• D. $\omega_2$ $V_{Q/P}$; direction of $V_{Q/P}$ rotated by $90^\circ$ opposite to the direction of $\omega_2$