A pinion with radius $r_1$, and inertia $I_1$ is driving a gear with radius $r_2$ and inertia $I_2$. Torque $\tau _1$ is applied on pinion. The following are free body diagrams of pinion and gear showing important forces ($F_1$ and $F_2$) of interaction. Which of the following relations hold true?
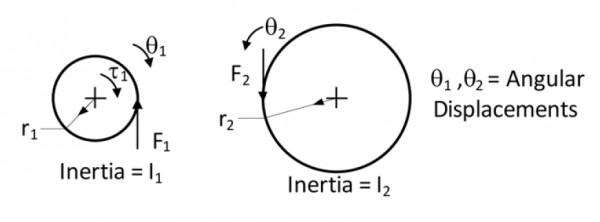
- $F_1\neq F_2;$ $\tau _1=I_1\ddot{\theta _1}$; $F_2=I_2\dfrac{r_1}{r_2^2}\ddot{\theta _1}; \\$
- $F_1=F_2$; $\tau _1= \big [ I_1+I_2 \left (\dfrac{r_1}{r_2} \right )^2 \big ]\ddot{\theta _1}$; $F_2=I_2\dfrac{r_1}{r_2^2}\ddot{\theta _1}; \\$
- $F_1=F_2;$ $\tau _1=I_1\ddot{\theta _1}$; $F_2=I_2\dfrac{1}{r_2}\ddot{\theta _1}; \\$
- $F_1\neq F_2$; $\tau _1= \big [I_1+I_2 \left (\dfrac{r_1}{r_2} \right )^2 \big ]\ddot{\theta _1}$; $F_2=I_2\dfrac{1}{r_2}\ddot{\theta _1};$