An epicyclic gear train is shown in the figure below. The number of teeth on the gears A, B and D are $20$, $30$ and $20$, respectively. Gear C has $80$ teeth on the inner surface and $100$ teeth on the outer surface. If the carrier arm AB is fixed and the sun gear A rotates at $300$ rpm in the clockwise direction, then the rpm of D in the clockwise direction is
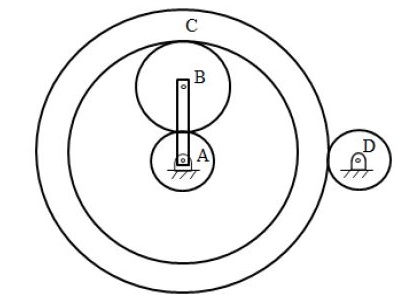
- $240$
- $-240$
- $375$
- $-375$