GATE Mechanical 2022 Set 2 | GA | Question: 9

Question

Four cities $\text{P, Q, R}$ and $\text{S}$ are connected through one-way routes as shown in the figure. The travel time between any two connected cities is one hour. The boxes beside each city name describe the starting time of first train of the day and their frequency of operation. For example, from city $\text{P}$, the first trains of the day start at $8\;\text{AM}$ with a frequency of $90$ minutes to each of $\text{R}$ and $\text{S}$. A person does not spend additional time at any city other than the waiting time for the next connecting train.

If the person starts from $\text{R}$ at $7\;\text{AM}$ and is required to visit $\text{S}$ and return to $\text{R}$, what is the minimum time required?

 

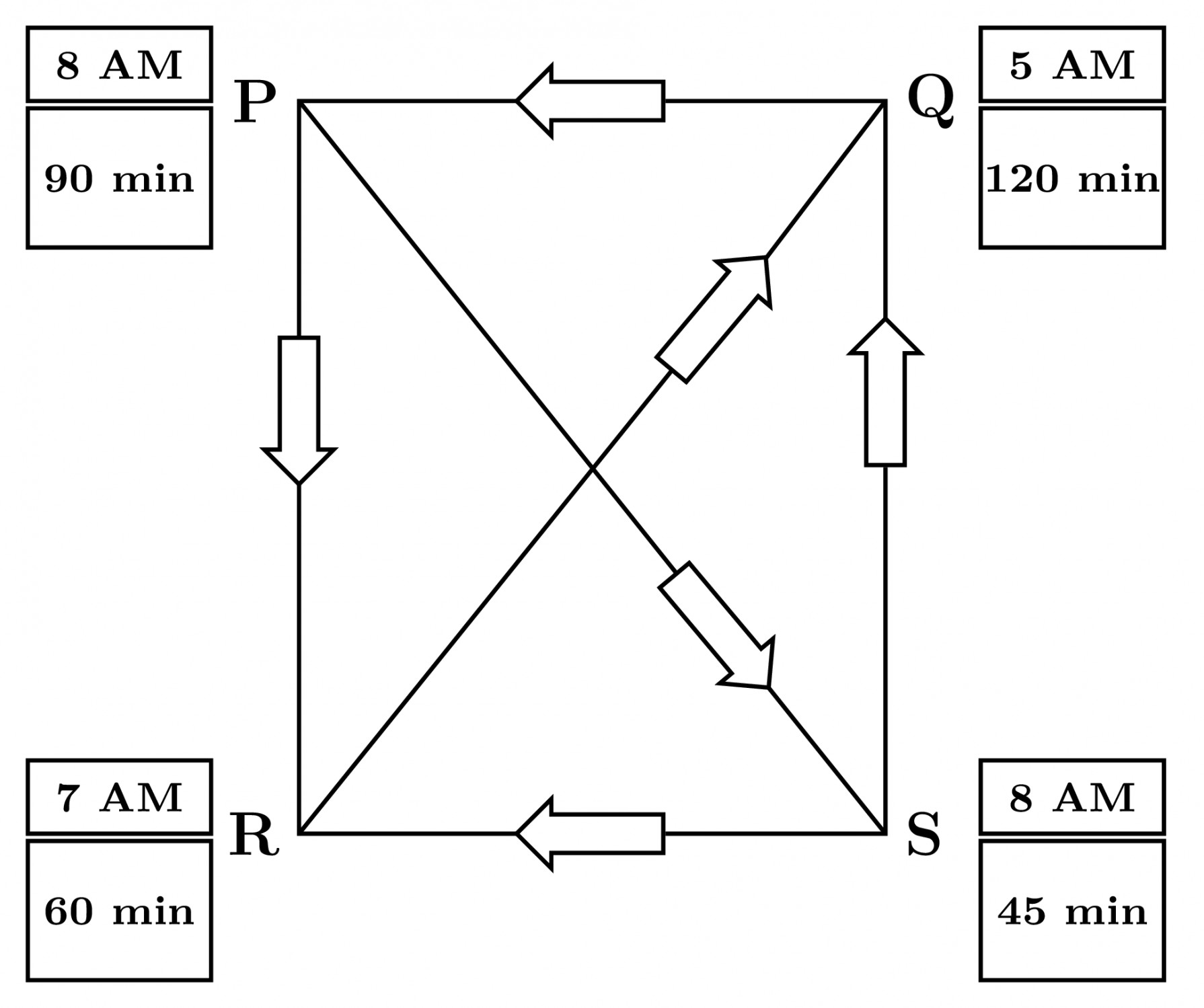
• A. $6$ hours $30$ minutes
• B. $3$ hours $45$ minutes
• C. $4$ hours $30$ minutes
• D. $5$ hours $15$ minutes

Answer 1

If the person starts from $\text{R}$ at $\text{7 AM}$ and is required to visit $\text{S}$ and return to $\text{R},$ then he must visit $\text{Q}$ and $\text{P}$ in between.

$\underbrace{\underbrace{\text{R}}_{{\color{Green}{\text{Start at: 7 AM}}}} \overset{\text{1 hour}}{\Longrightarrow} {\underbrace{\text{Q}}_{{\color{Red}{\text{Next train at: 9 AM}}}}} \overset{\text{1 hour}}{\Longrightarrow} \underbrace{\text{P}}_{{\color{Blue}{\text{Next train at: 11 AM}}}} \overset{\text{1 hour}}{\Longrightarrow} \underbrace{\text{S}}_{{\color{Purple}{\text{Next train at: 12:30 PM}}}} \overset{\text{1 hour}}{\Longrightarrow} \underbrace{\text{R}}_{{\color{Lime}{\text{Reach at: 1:30 PM}}}}}_{\text{Total time taken by person = 1 + 1 (waiting) + 1 + 1 (waiting)  + 1 +  ½ (waiting) + 1 = 6:30 hours}}$

$\therefore$ If the person starts from $\text{R}$ at $\text{7 AM}$ and is required to visit $\text{S}$ and return to $\text{R},$ then the minimum time required is $\text{6 hours 30 minutes}.$

Correct Answer $:\text{A}$

Comments

I have confusion in about Travelling time ? what is it?

Answer 2

Considered answer is option: A
which is 6hours 30minutes 
starting from R at 7AM and returned to R at 1:30PM with route R-Q-P-S-R
TIP: for example if we considered station R
so every 60min a train will be arrive at 8AM ,9AM ,10AM at station R
likewise for station Q every train will arrive with interval of 120min which is every 2hour example 5am ,7am and so on.
hope it helps for clearing doubt.☺