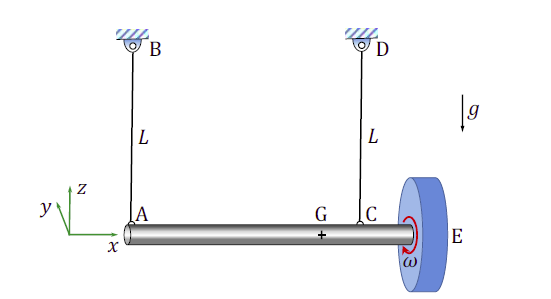
A massive uniform rigid circular disc is mounted on a frictionless bearing at the end $E$ of a massive uniform rigid shaft $\text{AE}$ which is suspended horizontally in a uniform gravitational field by two identical light inextensible strings $\text{AB}$ and $\text{CD}$ as shown, where $G$ is the center of mass of the shaft-disc assembly and $g$ is the acceleration due to gravity. The disc is then given a rapid spin $\omega$ about its axis in the positive $x$-axis direction as shown, while the shaft remains at rest. The direction of rotation is defined by using the right-hand thumb rule. If the string $\text{AB}$ is suddenly cut, assuming negligible energy dissipation, the shaft $\text{AE}$ will
- rotate slowly (compared to $\omega$) about the negative $z$-axis direction
- rotate slowly (compared to $\omega$) about the positive $z$-axis direction
- rotate slowly (compared to $\omega$) about the positive $y$-axis direction
- rotate slowly (compared to $\omega$) about the negative $y$-axis direction