GATE Mechanical 2021 Set 1 | GA | Question: 9

Question

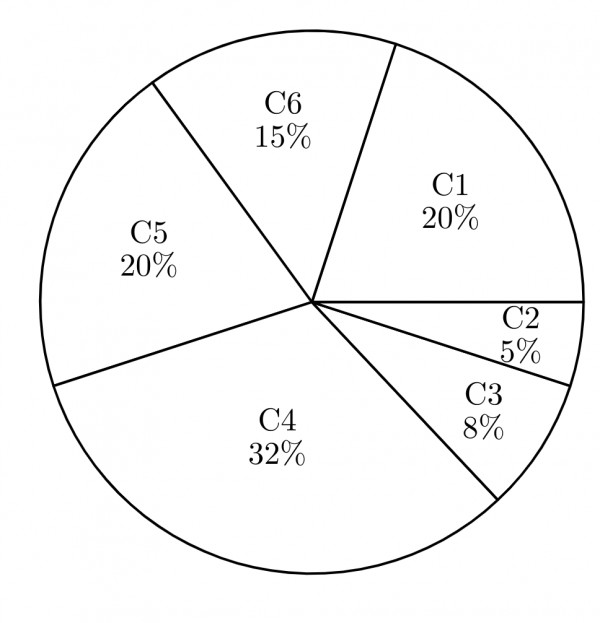
$$\begin{array}{|c|c|} \hline \textbf{Company} & \textbf{Ratio} \\\hline C1 & 3:2 \\\hline C2 & 1:4 \\\hline C3 & 5:3 \\\hline C4 & 2:3 \\\hline C5 & 9:1 \\\hline C6 & 3:4 \\\hline\end{array}$$

The distribution of employees at the rank of executives, across different companies $\textsf{C1, C2,} \ldots, \textsf{C6}$ is presented in the chart given above. The ratio of executives with a management degree to those without a management degree in each of these companies is provided in the table above. The total number of executives across all companies is $10,000.$

The total number of management degree holders among the executives in companies $\textsf{C2}$ and $\textsf{C5}$ together is ________.

• A. $225$
• B. $600$
• C. $1900$
• D. $2500$

Answer 1

Given that the total number of employees at the rank of executives across all companies is $10,000.$

• The number of employees in the company $C2 = \dfrac{5}{100} \times 10000 = 500$
• The number of employees in company $C2$, who has management degree $ = \dfrac{1}{5} \times 500 = 100$
• The number of employees in the company $C5 = \dfrac{20}{100} \times 10000 = 2000$
• The number of employees in company $C2$, who has management degree $ = \dfrac{9}{10} \times 2000 = 1800$

$\therefore$ The total number of management degree holders among the executives in companies $C2$ and $C5$ together $ = 100 + 1800 = 1900.$

So, the correct answer is $(C).$

Answer 2

Given that the total number of employees at the rank of executives across all companies is $10,000.$

• The number of employees in the company $C2 = \dfrac{5}{100} \times 10000 = 500$
• The number of employees in company $C2$, who has management degree $ = \dfrac{1}{5} \times 500 = 100$
• The number of employees in the company $C5 = \dfrac{20}{100} \times 10000 = 2000$
• The number of employees in company $C2$, who has management degree $ = \dfrac{9}{10} \times 2000 = 1800$

$\therefore$ The total number of management degree holders among the executives in companies $C2$ and $C5$ together $ = 100 + 1800 = 1900.$

So, the correct answer is $(C).$