Register

GATE Mechanical 2014 Set 2 | Question: 11

• recategorized by
0 votes
0 votes

A thin plate of uniform thickness is subject to pressure as shown in the figure below

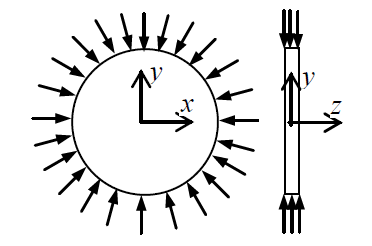
Under the assumption of plane stress, which one of the following is correct?

  1. Normal stress is zero in the z-direction
  2. Normal stress is tensile in the z-direction
  3. Normal stress is compressive in the z-direction
  4. Normal stress varies in the z-direction
• recategorized by
User Avatar

Please log in or register to answer this question.

← PreviousNext →
← Previous in categoryNext in category →
Answer:

Related questions

0 answers
0 votes
Arjun asked Feb 24, 2017
GATE2015-2-34
In a plane stress condition, the components of stress at a point are $\sigma_x =20$ $MPa$, $\sigma _y=80$ $MPa$ and $\tau_ {xy}$=$40$ $MPa$ The maximum shear stress (in $MPa$) at the point is $20$ $25$ $50$ $100$
In a plane stress condition, the components of stress at a point are $\sigma_x =20$ $MPa$, $\sigma _y=80$ $MPa$ and $\tau_ {xy}$=$40$ $MPa$ The maximum shear stress (in $...
Voting & Accepting an answer helps improve the community
Link Copied!