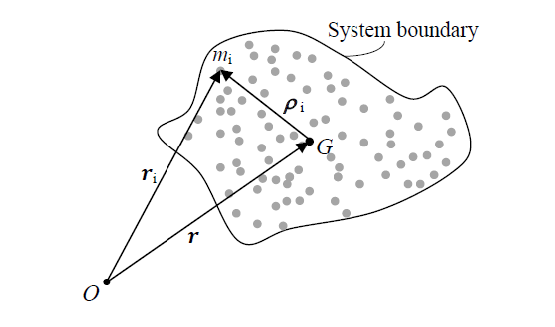
A system of particles in motion has mass center $G$ as shown in the figure. The particle $i$ has mass $m_i$ and its position with respect to a fixed point $O$ is given by the position vector $r_i$. The position of the particle with respect to $G$ is given by the vector $\rho _i$. The time rate of change of the angular momentum of the system of particles about $G$ is
(The quantity $\ddot{\rho _i}$ indicates second derivative of $\dot{\rho _i}$ with respect to time and likewise for $r_i$ ).
- $\sum _ir_i\times m_i\ddot{\rho _i}$
- $\sum _i\rho _i\times m_i\ddot{r_i}$
- $\sum _ir _i\times m_i\ddot{r_i}$
- $\sum _i\rho _i\times m_i\ddot{\rho _i}$