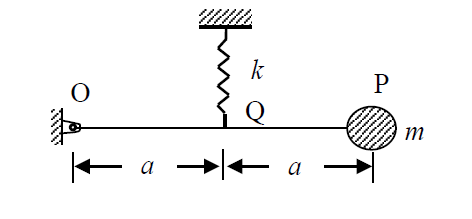
0 0 votes Figure shows a single degree of freedom system. The system consists of a massless rigid bar $OP$ hinged at $O$ and a mass $m$ at end $P$. The natural frequency of vibration of the system is $f_n=\displaystyle{\frac{1}{2\pi }\sqrt{\frac{k}{4m}}} \\$ $f_n=\displaystyle{\frac{1}{2\pi }\sqrt{\frac{k}{2m}}} \\$ $f_n=\displaystyle{\frac{1}{2\pi }\sqrt{\frac{k}{m}}} \\$ $f_n=\displaystyle{\frac{1}{2\pi }\sqrt{\frac{2k}{m}}}$ Vibrations gateme-2015-set3 vibrations applied-mechanics-and-design + – ♦Arjun 825 views answer comment Share Follow Add Sync Questions 0 reply Please log in or register to add a comment.
0 0 votes B is the answer. Phuawsd answered Jul 13, 2024 Phuawsd comment Share Follow 0 reply Please log in or register to add a comment.
