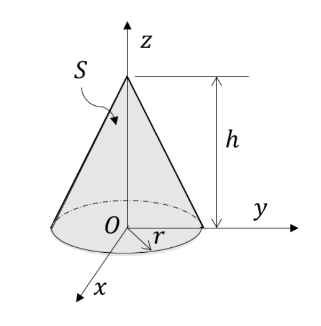
A vector field
$$
\mathbf{B}(x, y, z)=x \; \hat{\imath}+y \; \hat{\jmath}-2 z \; \hat{\mathrm{k}}
$$
is defined over a conical region having height $h=2$, base radius $r=3$ and axis along $z$, as shown in the figure. The base of the cone lies in the $x-y$ plane and is centered at the origin.
If $\boldsymbol{n}$ denotes the unit outward normal to the curved surface $S$ of the cone, the value of the integral
$$
\int_S \mathbf{B} \cdot \boldsymbol{n} \; \mathrm{dS}
$$
equals____________. (Answer in integer)