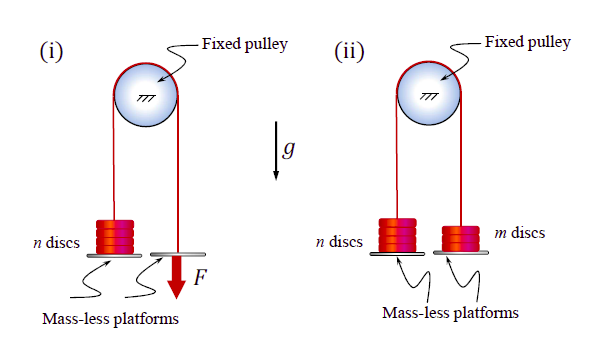
A rope with two mass-less platforms at its two ends passes over a fixed pulley as shown in the figure. Discs with narrow slots and having equal weight of $20\: N$ each can be placed on the platforms. The number of discs placed on the left side platform is $n$ and that on the right side platform is $m$.
It is found that for $n =5$ and $m = 0$, a force $F= 200 \:N$ (refer to part $\text{(i)}$ of the figure) is just sufficient to initiate upward motion of the lett side platform. If the force $F$ is removed then the minimum value of m (refer to part $\text{(ii)}$ of the figure) required to prevent downward motion of the left side platform is _____________________(in integer).