GATE Mechanical 2022 Set 2 | Question: 28

Question

A linear elastic structure under plane stress condition is subjected to two sets of loading, $\text{I}$ and $\text{II}$. The resulting states of stress at a point corresponding to these two loadings are as shown in the figure below. If these two sets of loading are applied simultaneously, then the net normal component of stress $\sigma _{xx}$ is __________________.

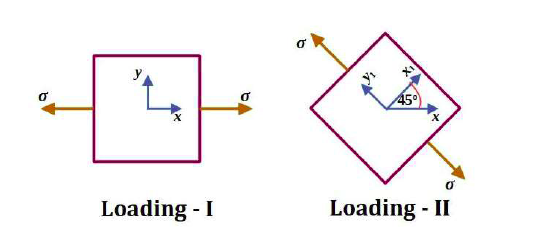
• A. $3\sigma /2$
• B. $\sigma \left ( 1+1/\sqrt{2} \right )$
• C. $\sigma /2$
• D. $\sigma \left ( 1-1/\sqrt{2} \right )$

Answer 1

Sigma cos^2 0+ sigma cos^2 45= net sigmaxx