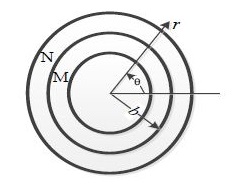
Consider two concentric circular cylinders of different materials $M$ and $N$ in contact with each other at $r=b$, as shown below. The interface at $r=b$ is frictionless. The composite cylinder is subjected to internal pressure $P$. Let $(u_r^M, u_{\theta}^M)$ and $(\sigma_{rr}^M, \sigma_{\theta \theta}^M)$ denote the radial and tangential displacement and stress components, respectively, in material $M$. Similarly, $(u_r^N, u_{\theta}^N)$ and $(\sigma_{rr}^N, \sigma_{\theta \theta}^N)$ denote the radial and tangential displacement and stress components, respectively, in material $N$. The boundary conditions that need to be satisfied at the frictionless interface between the two cylinders are:
- $u_r^M = u_r^N \text{ and } \sigma_{rr}^M = \sigma_{rr}^N \text{ only}$
- $u_r^M = u_r^N \text{ and } \sigma_{rr}^M = \sigma_{rr}^N \text{ and } u_{\theta}^M = u_{\theta}^N \text{ and } \sigma_{\theta \theta}^M = \sigma_{\theta \theta}^N$
- $u_{\theta}^M = u_{\theta}^N \text{ and } \sigma_{\theta \theta}^M = \sigma_{\theta \theta}^N $
- $\sigma_{rr}^M = \sigma_{rr}^N \text{ and } \sigma_{\theta \theta}^M = \sigma_{\theta \theta}^N$