Consider one-dimensional steady state heat conduction, without heat generation, in a plane wall; with boundary conditions as shown in the figure below. The conductivity of the wall is given by $k$ = $k_0$ + $bT$ ; where $k_0$ and $b$ are positive constants, and $T$ is temperature.
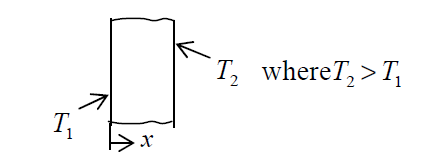
As $x$ increases, the temperature gradient ( $dT$/ $dx$ ) will
- remain constant
- be zero
- increase
- decrease