A square plate of dimension $L \times L$ is subjected to a uniform pressure load $p=250 \: MPa$ on its edges as shown in the figure. Assume plane stress conditions. The Young’s modulus $E=200 \: GPa$
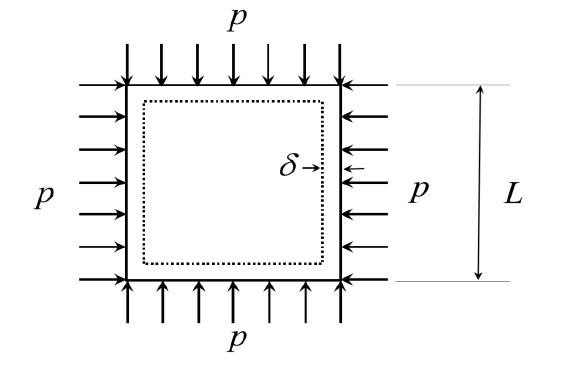
.The deformed shape is a square of dimension $L− 2\delta$. If $L = 2 \: m$ and $\delta=0.001 \: m$, the Poisson’s ratio of the plate material is __________