A solid disc with radius $a$ is connected to a spring at a point $d$ above the center of the disc. The other end of the spring is fixed to the vertical wall. The disc is free to roll without slipping on the ground. The mass of the disc is $M$ and the spring constant is $K$. The polar moment of inertia for the disc about its centre is $J = \displaystyle{\frac{Ma^2}{2}}$ .
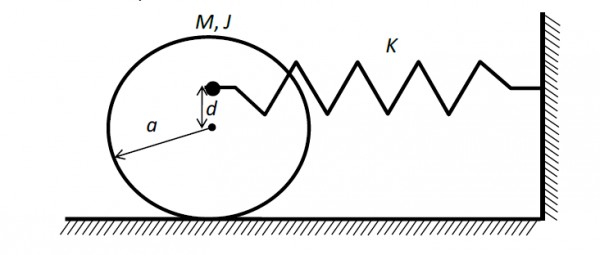
The natural frequency of this system in $\text {rad} / \text {s}$ is given by
- $\displaystyle{\sqrt{\frac{2K(a+d)^2}{3Ma^2}}} \\$
- $\displaystyle{\sqrt{\frac{2K}{3M}}} \\$
- $\displaystyle{\sqrt{\frac{2K(a+d)^2}{Ma^2}}} \\$
- $\displaystyle{\sqrt{\frac{K(a+d)^2}{Ma^2}}}$