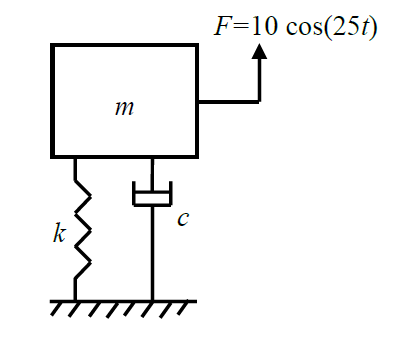
A mass-spring-dashpot system with mass $m = 10$ $kg$, spring constant $k = 6250$ $N/m$ is excited by a harmonic excitation of $10 cos(25t)$ $N$. At the steady state, the vibration amplitude of the mass is $40$ $mm$. The damping coefficient ($c$, in $N.s/m$) of the dashpot is _______