Fluidity of a molten alloy during sand casting depends on its solidification range. The phase diagram of a hypothetical binary alloy of components $A$ and $B$ is shown in the figure with its eutectic composition and temperature. All the lines in this phase diagram, including the solidus and liquidus lines, are straight lines. If this binary alloy with $15$ weight $\%$ of $B$ is poured into a mould at a pouring temperature of $800^{\circ}C$, then the solidification range is
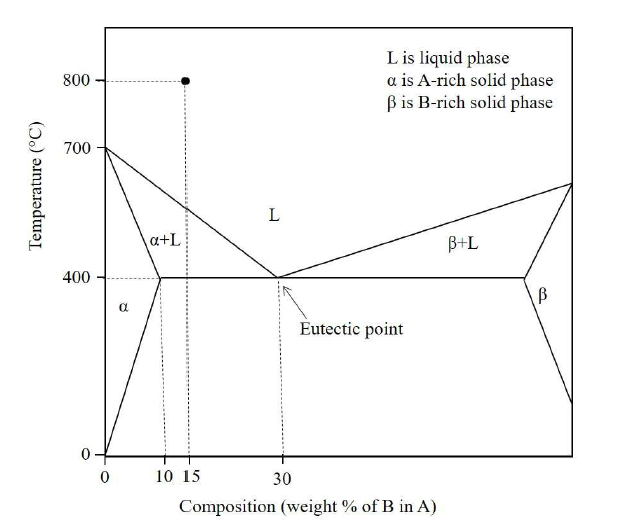
- $400^{\circ}C$
- $250^{\circ}C$
- $800^{\circ}C$
- $150^{\circ}C$