A spring mass damper system (mass $m$, stiffness $k$, and damping coefficient $c$) excited by a force $F(t) = B \sin w t$, where $B$, $w$ and $t$ are the amplitude, frequency and time, respectively, is shown in the figure. Four different responses of the system (marked as $\text{(i)}$ to $\text{(iv)}$) are shown just to the right of the system figure. In the figures of the responses, $A$ is the amplitude of response shown in red color and the dashed lines indicate its envelope. The responses represent only the qualitative trend and those are not drawn to any specific scale.
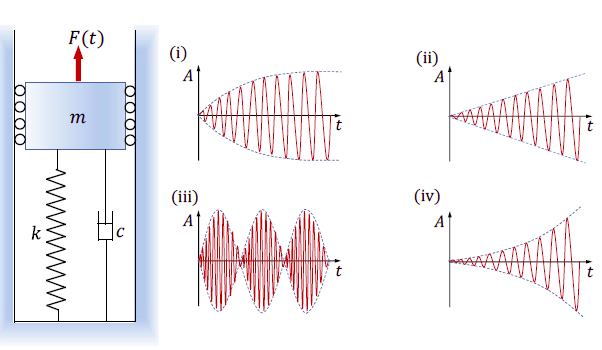
Four different parameter and forcing conditions are mentioned below.
$(P)$ $c>0$ and $w = \sqrt{k/m}$
$(Q)$ $c<0$ and $w \neq 0$
$(R)$ $c=0$ and $w = \sqrt{k/m}$
$(S)$ $c=0$ and $w \cong \sqrt{k/m}$
Which one of the following options gives correct match (indicated by arrow $\rightarrow$) of the parameter and forcing conditions to the response?
- $(P) \rightarrow \text{(i)}, (Q) \rightarrow \text{(iii)}, (R) \rightarrow \text{(iv)}, (S) \rightarrow \text{(ii)}$
- $(P) \rightarrow \text{(ii)}, (Q) \rightarrow \text{(iii)}, (R) \rightarrow \text{(iv)}, (S) \rightarrow \text{(i)}$
- $(P) \rightarrow \text{(i)}, (Q) \rightarrow \text{(iv)}, (R) \rightarrow \text{(ii)}, (S) \rightarrow \text{(iii)}$
- $(P) \rightarrow \text{(iii)}, (Q) \rightarrow \text{(iv)}, (R) \rightarrow \text{(ii)}, (S) \rightarrow \text{(i)}$