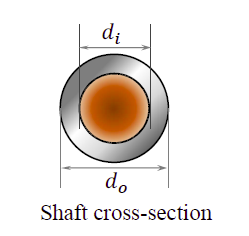
A shaft of length $L$ is made of two materials, one in the inner core and the other in the outer rim, and the two are perfectly joined together (no slip at the interface) along the entire length of the shaft. The diameter of the inner core is $d_{i}$ and the external diameter of the rim is $d_{o}$, as shown in the figure. The modulus of rigidity of the core and rim materials are $G_{i}$ and $G_{o}$, respectively. It is given that $d_{o} = 2d_{i}$ and $G_{i} = 3G_{o}$. When the shaft is twisted by application of a torque along the shaft axis, the maximum shear stress developed in the outer rim and the inner core turn out to be $\tau_{o}$ and $\tau_{i}$, respectively. All the deformations are in the elastic range and stress-strain relations are linear. Then the ratio $\tau_{i}/ \tau_{o}$ is ______________ (round off to $2$ decimal places).
Gurdeep Saini
~^~Dbnjn