First, we can draw the diagram.
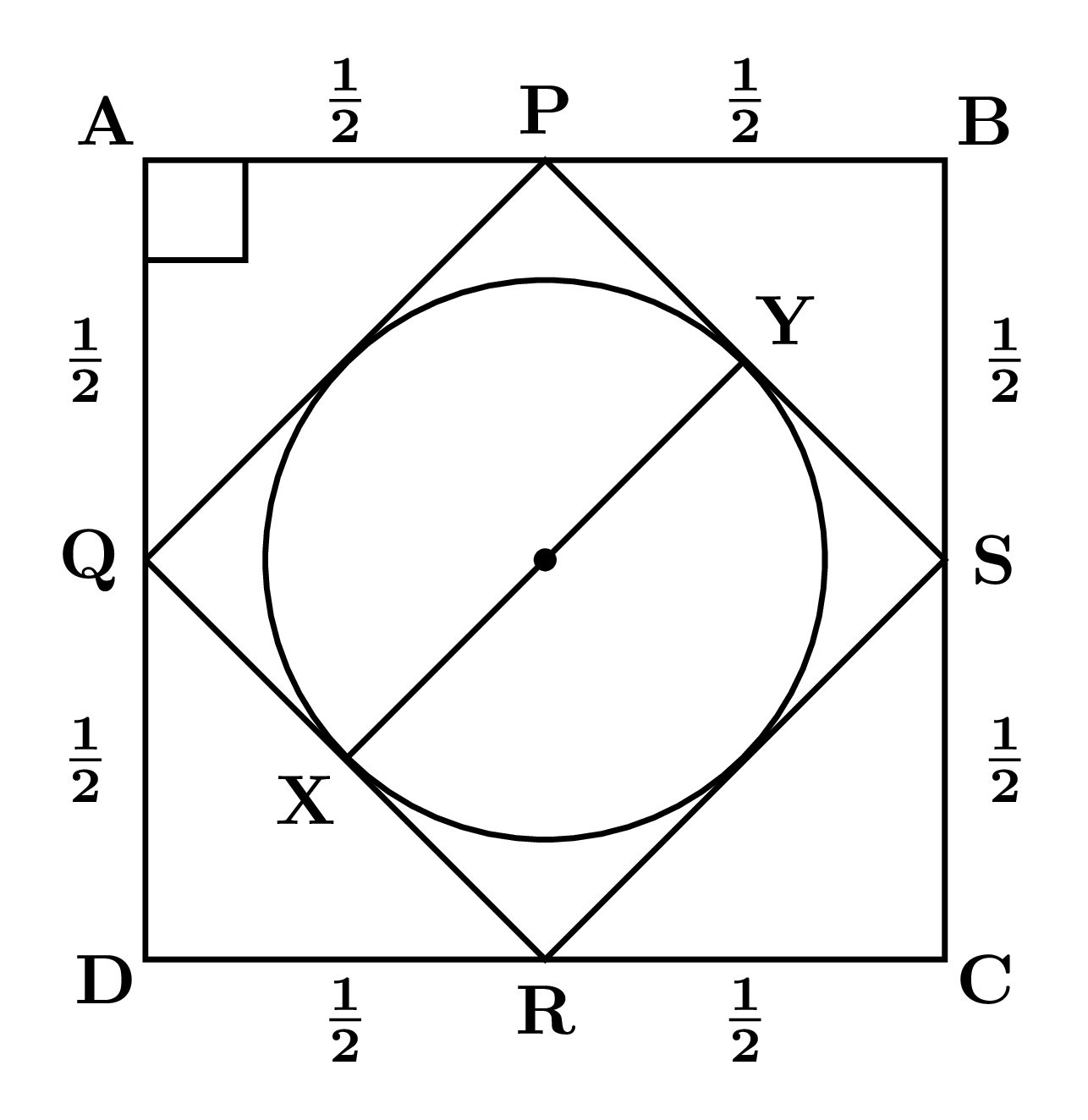
$\triangle \text{PAQ}$ is a right-angle triangle. So we can apply the Pythagorean theorem.
${\color{Green}{(\text{Hypotenuse})^{2} = (\text{Perpendicular})^{2} + (\text{Base})^{2}}}$
$\Rightarrow (\text{PQ})^{2} = (\text{AQ})^{2} + (\text{AP})^{2}$
$\Rightarrow (\text{PQ})^{2} = \left(\frac{1}{2}\right)^{2} + \left(\frac{1}{2}\right)^{2}$
$\Rightarrow \text{PQ} = \sqrt{\frac{1}{4} + \frac{1}{4}}$
$\Rightarrow \text{PQ} = \sqrt{\frac{2}{4}}$
$\Rightarrow \text{PQ} = \sqrt{\frac{1}{2}}$
$\Rightarrow {\color{Blue}{\boxed{ \text{XY} = \frac{1}{\sqrt{2}}}}} \quad [{\color{Red}{\because \text{PQ = XY}}}]$
$\therefore$ The diameter of the largest circle that can be inscribed within the rhombus is $ \dfrac{1}{\sqrt{2}}.$
Correct Answer $:\text{A}$