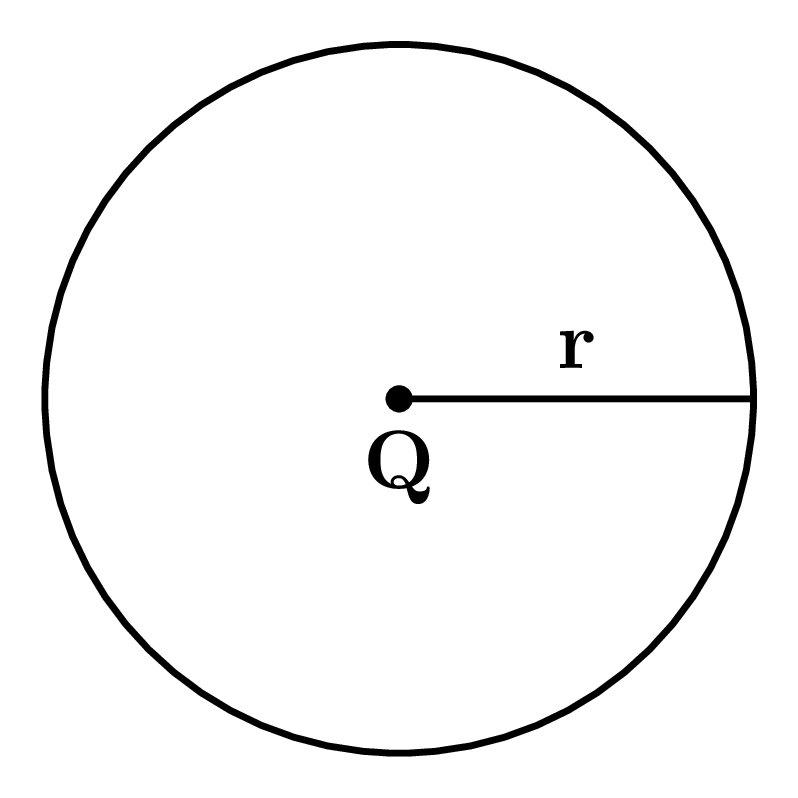
Let the side of an equilateral triangle, side of a square, the radius of a circle be $a,x,$ and $r$ respectively.
Now, $\frac{\sqrt{3}}{4}\; a^{2} = x^{2} = \pi r^{2} = k^{2}\;(\text{let})$
Now,
- $\frac{\sqrt{3}}{4}\; a^{2} = k^{2} \Rightarrow a^{2} = \frac{4k^{2}}{\sqrt{3}} \Rightarrow {\color{Blue}{\boxed{a = \frac{2k}{\sqrt{\sqrt{3}}}}}}$
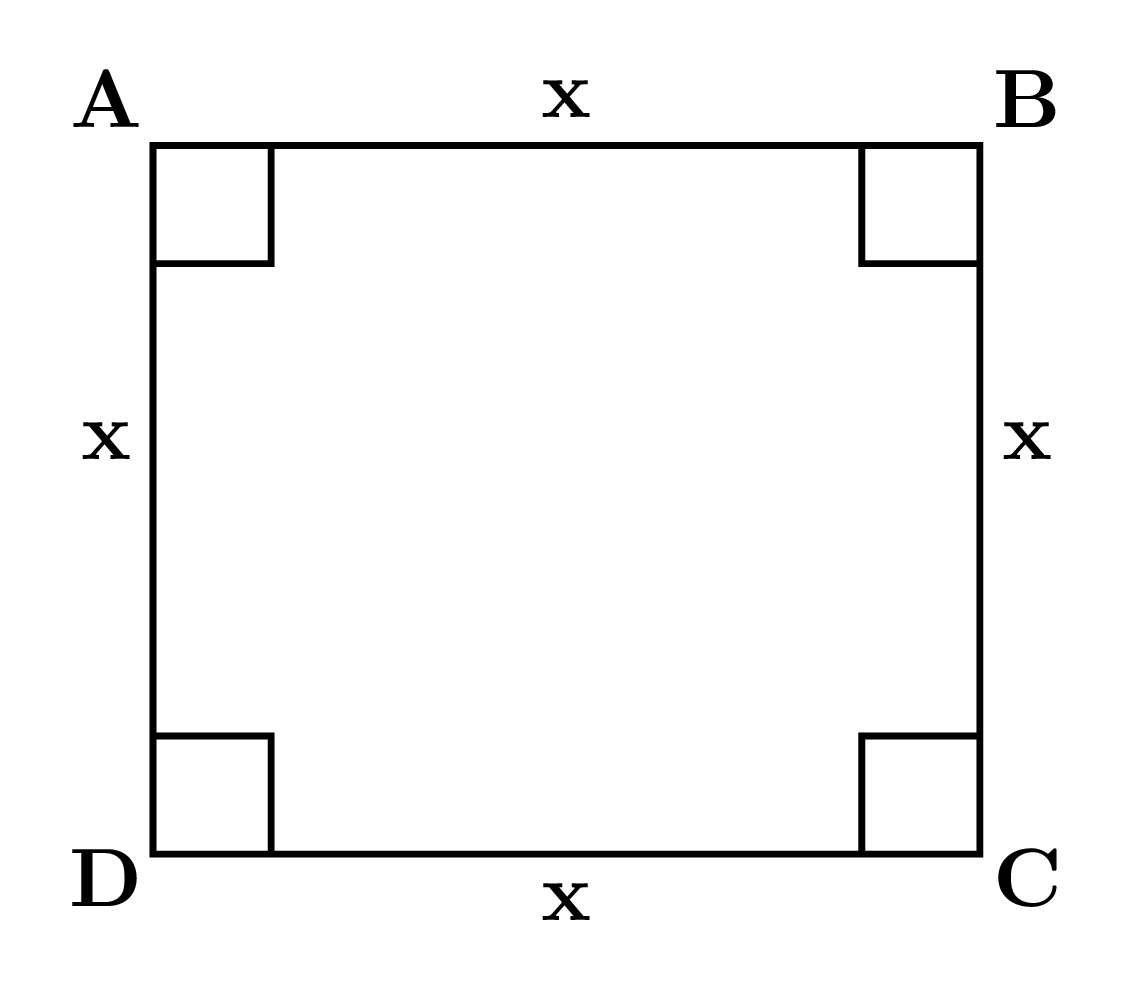
- $x^{2} = k^{2} \Rightarrow {\color{Purple}{\boxed{x = k}}}$
- $\pi r^{2} = k^{2} \Rightarrow {\color{Teal}{\boxed{r = \frac{k}{\sqrt{\pi}}}}}$
Now, we can calculate the perimeter of each of that.
- The perimeter of an equilateral triangle $ = 3a$
- The perimeter of a square $ = 4x$
- The perimeter of a circle $ = 2\pi r$
The ratio of the perimeters of the equilateral triangle to square to circle $ = 3a:4x:2\pi r$
$\qquad \qquad = 3 \times \dfrac{2k}{\sqrt{\sqrt{3}}} : 4k:2 \pi \times \dfrac{k}{\sqrt{\pi}}$
$\qquad \qquad = \dfrac{3}{\sqrt{\sqrt{3}}} \times \dfrac{\sqrt{\sqrt{3}}}{\sqrt{\sqrt{3}}} : 2: \sqrt{\dfrac{\pi ^{2}}{ \pi}}$
$\qquad \qquad = \dfrac{3\;\sqrt{\sqrt{3}}}{\sqrt{3}} : 2: \sqrt{\pi}$
$\qquad \qquad = \dfrac{3\;\sqrt{\sqrt{3}}}{\sqrt{3}} \times \dfrac{\sqrt{3}}{\sqrt{3}} : 2: \sqrt{\pi}$
$\qquad \qquad = \sqrt{(3 \sqrt{3})}:2:\sqrt{\pi}$
Correct Answer $:\text{B}$
$\textbf{Important Points:}$
- The area of an equilateral triangle ${\color{Green}{ = \dfrac{\sqrt{3}}{4}\;(\text{Side of an equilateral triangle})^{2}}}$

- The area of a square ${\color{Lime}{ = (\text{Side of a square})^{2}}}$
- The area of a circle ${\color{Cyan}{= (\text{Radius})^{2}}}$