Given that a square sheet has a side length of $1$ unit.
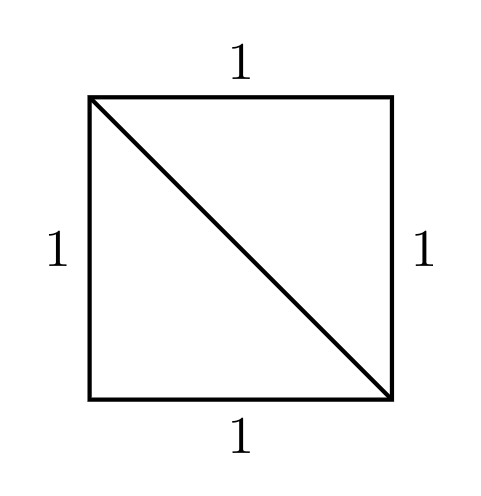
Now, the sheet is first folded along the main diagonal.
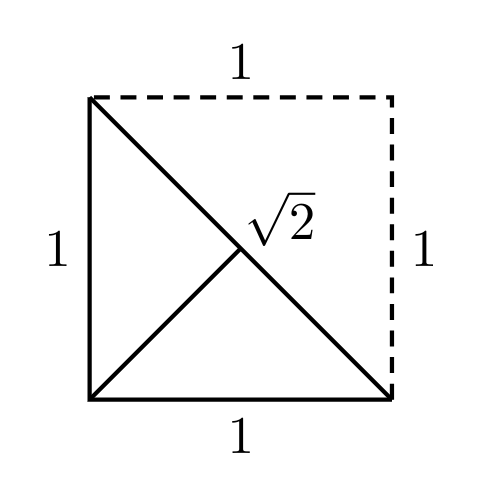
Again, this is followed by a fold along its line of symmetry. And this operation is performed two times.
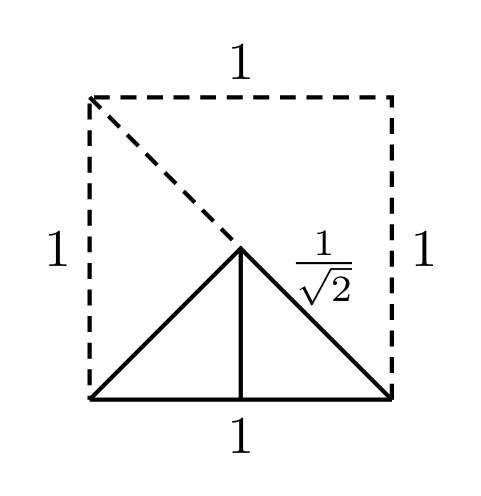
We get the final folded sheet.
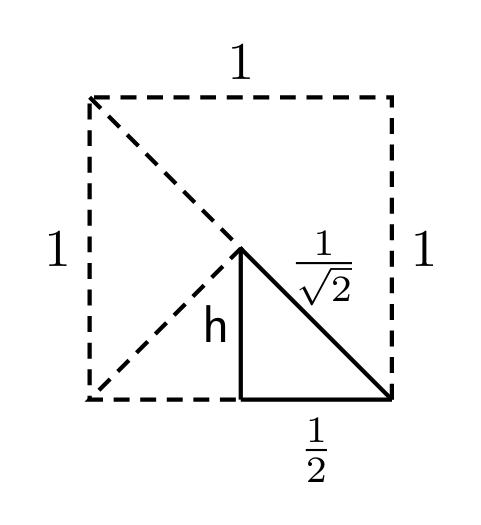
Let the height of the triangle be $h$ units.
Using the Pythagorean theorem, we get.
$\left(\frac{1}{\sqrt{2}}\right)^{2} = h^{2} + \left(\frac{1}{2}\right)^{2}$
$\implies \frac{1}{2} = h^{2} + \frac{1}{4}$
$\implies h^{2} = \frac{1}{2} – \frac{1}{4}$
$\implies h^{2} = \frac{2 – 1 }{4} = \frac{1}{4}$
$\implies h = \frac{1}{2}$
Now, the area of triangle $\Delta = \frac{1}{2} \times \text{Base} \times \text{Height}$
$\implies \Delta = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}\;\text{unit}^{2}.$
$\textbf{Short Method:}$ Area follows the symmetry.
- Initially the area of square $ = 1$
- Folded first time, then the area of square $ = \frac{1}{2}$
- Folded second time, then the area of square $ = \frac{1}{4}$
- Folded third time, then the area of square $ = \frac{1}{8}$
So, the correct answer is $(B).$