Register

GATE Mechanical 2020 Set 1 | GA Question: 9

• edited by

1 Answer

Best answer
1 votes
1 votes

Given that $y_1 = x^{m}\;;\; 0\leq x \leq 1,\; m>1$

For simplicity we can take $m = 2,$ differentiate the function and get the slope.

For $y = x^{2}$ we get $m_1 = \frac{\mathrm{d} y }{\mathrm{d} x} = 2x.$

Similarly for $y_2 = x^{1/2}$ we get $m_2 = \frac{\mathrm{d} y }{\mathrm{d} x} = \frac{1}{2\sqrt x}$

At $x = 0, m_1 = 0, m_2 = \infty$

At $x = 1, m_1 = 2, m_2 = 0.5$ 

Only for option, A slope of $y_1$ is increasing and slope of $y_2$ is decreasing.

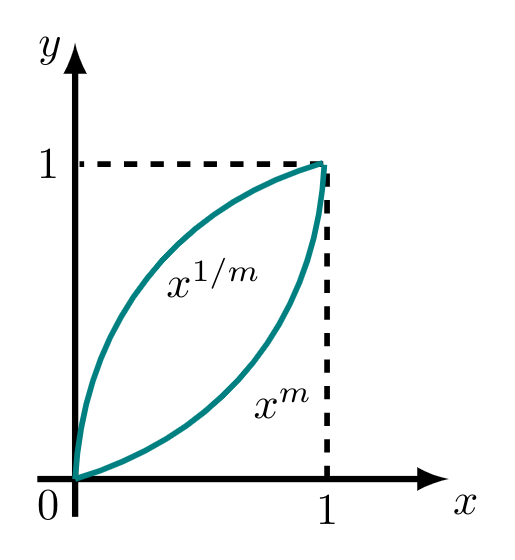
So, the correct answer is $(A).$

• edited by
User Avatar
← PreviousNext →
← Previous in categoryNext in category →
Answer:

Related questions

1 answers
1 votes
go_editor asked Feb 19, 2020
GATE Mechanical 2020 Set 1 | GA Question: 5
Define $[x]$ as the greatest integer less than or equal to $x$, for each $x\in \left (- \infty, \infty \right ).$ If $y = [x]$, then area under $y$ for $x\in \left [ 1,4 \right ]$ is _______. $1$ $3$ $4$ $6$
Define $[x]$ as the greatest integer less than or equal to $x$, for each $x\in \left (- \infty, \infty \right ).$ If $y = [x]$, then area under $y$ for $x\in \left [ 1,4 ...
0 answers
0 votes
Arjun asked Feb 24, 2017
GATE Mechanical 2016 Set 2 | GA Question: 10
Which of the following curves represents the function $ln(|e^{[|\sin(|x|)]}|)$ for $\mid x\mid< 2\pi$? Here, $x$ represents the abscissa and $y$ represents the ordinate.
Which of the following curves represents the function $ln(|e^{[|\sin(|x|)]}|)$ for $\mid x\mid< 2\pi$? Here, $x$ represents the abscissa and $y$ represents the ordinate.
1 answers
1 votes
go_editor asked Feb 19, 2020
GATE Mechanical 2020 Set 1 | GA Question: 8
The sum of the first $n$ terms in the sequence $8,\:88,\:888,\:8888,\dots$ is ________. $\dfrac{81}{80}\left ( 10^{n}-1 \right )+\dfrac{9}{8}n \\$ $\dfrac{81}{80}\left ( 10^{n}-1 \right )-\dfrac{9}{8}n \\$ $\dfrac{80}{81}\left ( 10^{n}-1 \right )+\dfrac{8}{9}n \\$ $\dfrac{80}{81}\left ( 10^{n}-1 \right )-\dfrac{8}{9}n$
The sum of the first $n$ terms in the sequence $8,\:88,\:888,\:8888,\dots$ is ________.$\dfrac{81}{80}\left ( 10^{n}-1 \right )+\dfrac{9}{8}n \\$$\dfrac{81}{80}\left ( 10...
0 answers
0 votes
Arjun asked Feb 19, 2017
GATE Mechanical 2014 Set 4 | GA Question: 4
Let $f(x,y)=x^n y^m=P$ If $x$ is doubled and $y$ is halved, the new value of $f$ is $2^{n-m}P$ $2^{m-n}P$ $2(n-m)P$ $2(m-n)P$
Let $f(x,y)=x^n y^m=P$ If $x$ is doubled and $y$ is halved, the new value of $f$ is$2^{n-m}P$$2^{m-n}P$$2(n-m)P$$2(m-n)P$
1 answers
1 votes
go_editor asked Feb 19, 2020
GATE Mechanical 2020 Set 1 | GA Question: 10
The bar graph shows the data of the students who appeared and passed in an examination for four schools $P, Q, R$, and $S$. The average of success rates $\text{(in percentage)}$ of these four schools is _______. $58.5\%$ $58.8\%$ $59.0\%$ $59.3\%$
The bar graph shows the data of the students who appeared and passed in an examination for four schools $P, Q, R$, and $S$. The average of success rates $\text{(in percen...
Voting & Accepting an answer helps improve the community
Link Copied!