A rigid mass-less rod of length $L$ is connected to a disc (pulley) of mass $m$ and radius $r = L/4$ through a friction-less revolute joint. The other end of that rod is attached to a wall through a friction-less hinge. A spring of stiffness $2k$ is attached to the rod at its mid-span. An inextensible rope passes over half the disc periphery and is securely tied to a spring of stiffness $k$ at point $C$ as shown in the figure. There is no slip between the rope and the pulley. The system is in static equilibrium in the configuration shown in the figure and the rope is always taut.
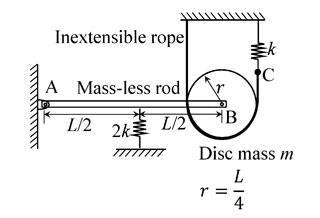
Neglecting the influence of gravity, the natural frequency of the system for small amplitude vibration is
- $\sqrt{\dfrac{3}{2}}\sqrt{\dfrac{k}{m}} \\$
- ${\dfrac{3}{\sqrt{2}}}\sqrt{\dfrac{k}{m}}\\$
- $\sqrt{3}\sqrt{\dfrac{k}{m}} \\$
- $\sqrt{\dfrac{k}{m}}$