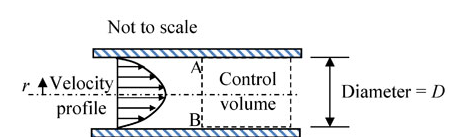
Consider steady, viscous, fully developed flow of a fluid through a circular pipe of internal diameter $\text{D}$. We know that the velocity profile forms a paraboloid about the pipe centre line, given by: $V=-C\left(r^{2}-\dfrac{D^{2}}{4}\right) m/s$, where $C$ is a constant. The rate of kinectic energy $(\text{in}\: J/s)$ at the control surface $\text{A-B}$, as shown in the figure, is proportional to $D^{n}$. The value of $n$ is ________.