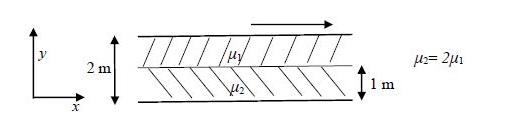
Two immiscible, incompressible, viscous fluids having same densities but different viscosities are contained between two infinite horizontal parallel plates, $2 \: m$ apart as shown below. The bottom plate is fixed and the upper plate moves to the right with a constant velocity of $3 \: m/s$. With the assumptions of Newtonian fluid, steady, and fully developed laminar flow with zero pressure gradient in all directions, the momentum equations simplify to
$$\frac{d^2u}{dy^2}=0$$
If the dynamic viscosity of the lower fluid, $\mu_2$, is twice that of the upper fluid, $\mu_1$, then the velocity at the interface (round off to two decimal places) is _______ $m/s$.